Nekonečný hotel má ubytovaných nekonečno ľudí. No čo ak príde ďalší hosť?
Letné prázdniny sa (našťastie) veľmi rýchlo približujú a s nimi sú spojené aj dovolenky a ubytovania v rôznych hoteloch. Komu by sa nepáčil päťhviezdičkový hotel na pláži na vašom vysnívanom mieste? Napriek tomu sa dnes nebudeme venovať cestovnému ruchu ani ubytovaniu, ale niečomu, čo fascinuje ľudí už oddávna - nekonečno.
Nemec David Hilbert (1862 - 1943) bol jedným z najzaslúženejších matematikov vtedajšej doby. Okrem mimoriadneho úspechu na mnohých poliach predniesol niečo, čo sa dnes označuje ako Hilbertov paradox. Vďaka nemu zjednodušil pojem nekonečna a v hlave si postavil naozaj veľký hotel.

Nekonečno
Najprv však pár jednoduchých faktov o nekonečne. Je zaujímavé, že sa o ňom každý vyjadruje ako o čísle, no na číselnej osi sa skrátka nenachádza. Vieme len, že je niekde ďaleko vpravo na konci osi a potom ešte kúsok. No a to je prvá chyba. Nekonečno je číselná os celá - všetky tie celé čísla ako 5, 6, 7, 8..., je ich tam skrátka nekonečno. To je prvé nekonečno, o ktorom vieme spoľahlivo hovoriť, že nemá koniec, kedže nech napíšeme akékoľvek číslo, vieme k nemu vždy pridať jednotku (n+1). Mimochodom, tomuto typu nekonečna sa hovorí spočítateľné alebo "countable infinity".
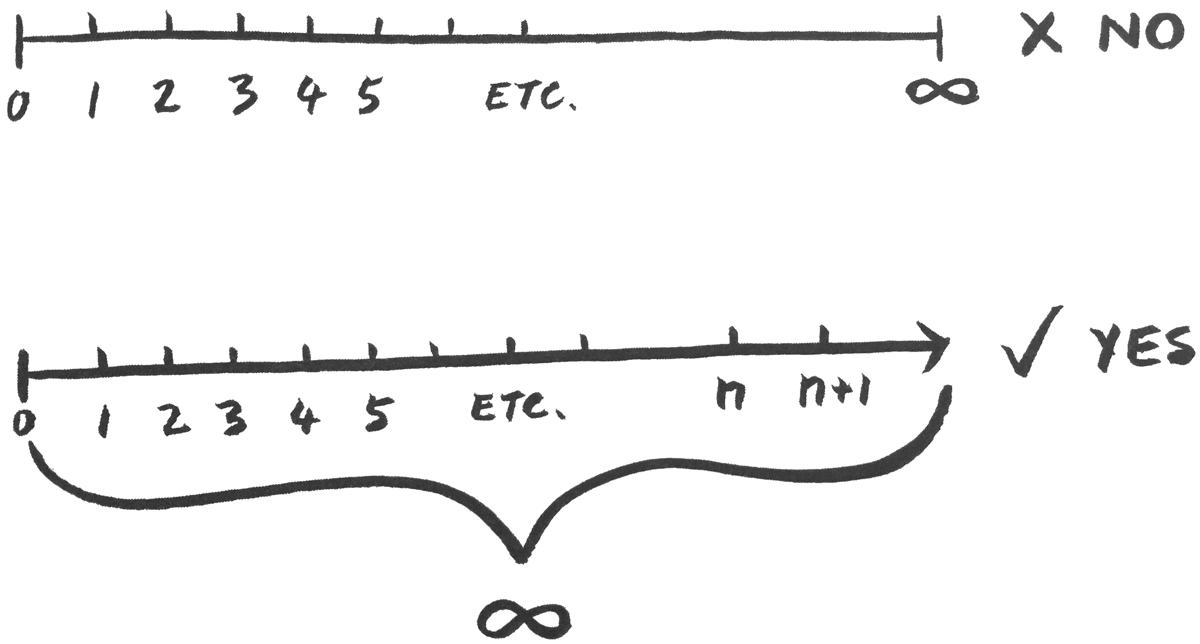
Určite každému teraz napadne, že existuje ešte viac hardcore level nekonečna. Na číselnej osi sú medzi celými číslami prázdne kúsky, v ktorých sú čísla s desatinnou čiarkou. A tých je tam nekonečno. V nekonečnom počte prázdnych kúskov medzi dvomi celými číslami. To sa zdá ako nekonečno2 alebo nekonečnonekonečno ale to, že ide len o to bežné nekonečno, vysvetlíme neskôr.
My si však dovolíme ešte priliať do ohňa a spýtame sa - napíš všetky čísla od nuly. Prvá bude teda nula. Ale čo nasleduje? Bude to 0.0001? Alebo snáď 0.00000001? Možností je nekonečno. Toto je zasa nespočítateľné nekonečno, alebo kontinuum.
Na záver krátkeho informačného okienka ešte posledná vec a potom už bude hotel, sľubujeme. Ak máš kôpku 7 cukríkov a jeden tam pridáš, máš ich 8, to by mala väčšina ľudí akceptovať. No ak máš nekonečno cukríkov a k tomu pridáš cukrík, nemáš ∞ + 1 cukríkov, ale iba ∞, kedže ako sme si ukázali vyššie, nekonečno nie je číslo, nemožno k nemu pridávať. Detto ∞ krát ∞ je stále ∞.
Nekonečný hotel
Ujo Hilbert má hotel s nekonečným počtom izieb a ubytováva nekonečný počet hostí. Dve nekonečná sú si rovné a teda v každej izbe je jeden hosť. Izby sú označené číslami (1, 2...) a všetci hostia sú spokojní, no v tom na dvere zaklope muž, ktorý chce ďalšiu izbu. Čo teraz? Veď všetky izby sú obsadené, každé číslo má svojho hosťa. Koniec chodby s izbami nie je a Hilbert kvôli tomu nemá ako nového hosťa poslať na koniec chodby. S potenciálnym zákazníkom to veľmi dobre teda nevyzerá. Ale ujo Hilbert je slávny matematik a vynájde sa. Ubytovaného z izby 1 presunie do dvojky, hosťa z izby 2 do izby 3 a takto sa celý hotel presťahuje. Počet izieb je stále nekonečný, počet hostí je nekonečný a pravdepodobne bude nekonečný aj počet sťažností ubytovaných na tento nekonečne skvelý biznis.
Jedného hosťa teda Hilbert ubytuje a ubytoval by aj ďalších prichádzajúcich. Skrátka by všetkých hostí posunul ďalej. Čo ak však príde dovolenkový autobus s nekonečným počtom hostí? Ten totiž práve zaparkoval a tak treba veľmi rýchlo vymyslieť riešenie, ako ubytovať ďalšie nekonečno ľudí.
Už sme spomínali, že spočítateľné nekonečná sú rovnaké a teda ubytované nekonečno, nekonečno, ktoré sa chce dať ubytovať a aj finálne nekonečno by mali byť rovnaké. Teoreticky by sa to teda malo dať zvládnuť. Najprv si však dovolíme návrat k informačnému okienku a spýtame sa: Koľkokrát je všetkých kladných celých čísel viac ako všetkých párnych čísel?
Zdravý rozum a aj všetko ostatné kričí, že párnych čísel je predsa dvakrát menej, bohužiaľ je to opäť zle. Ani zoznam kladných, ani zoznam párnych čísel nemajú koniec, takže sú to obidve nekonečná - teda zhodné. Čiže existuje rovnako párnych čísel ako rovnako všetkých celých čísel. Mindblown.
Hilbert o tomto tuší, a tak presunie každého hosťa do izby s číslom dvakrát väčším ako je aktuálne číslo ubytovaného. Pán z dvojky ide na štvorku atď. Tým pádom sa uvoľní polovica všetkých izieb, kam napraceme to nekonečno, ktoré práve vystupuje z autobusu. Mimochodom, naozaj by sme nechceli bývať v izbe s číslom 682779 a sťahovať sa do dvakrát väčšieho čísla.
Hilbert je zrejme naozaj matematickým a logickým bohom, no chuť zákazníkov ubytovať sa v jedinečnom nekonečnom hoteli ešte stúpla, a tak na parkovisku zastalo nekonečno autobusov s nekonečným počtom hostí. Kedže v minulom príklade prišlo len nekonečno, domáci musel vytvoriť nekonečno izieb. Tu však treba vytvoriť nekonečno nekonečien izieb a ujo Hilbert sa už poriadne potí. Preto zavolá svojim dvom dobrým priateľom - Georgovi Gamowovi a Albertovi Einsteinovi. Spoločne prídu na to, že to naozaj ide. Už sa nachádzame v dobe, kedy vieme, že prvočísel (číslo deliteľné len 1 a samým sebou) je nekonečno. Mocniny prvočísla majú tú peknú vlastnosť, že potom už nie sú mocninou ďalšieho iného čísla. Teda napríklad druhá mocnina čísla 11 je 121 a tá sa nedá odmocniť do iného celého čísla okrem jedenástky.
Hilbert teda umiestni všetkých už-hostí do izieb, ktorých čísla sú mocninou prvého prvočísla. To je dvojka, zákazníci sa presunú do izieb 2, 4, 8, 16, 32.... Prvý autobus z nekonečna umiestni do izieb, ktoré sú mocninou druhého prvočísla v rade, to je trojka. Obsadené sú teda izby 3, 9, 27, 81... Ďalšie prvočíslo je 5, teda sa obsadia izby 5, 25, 125... A tak ďalej.
A tu celý myšlienkový experiment vystupujúci pod názvami Hilbertov paradox, Hilberov Grand Hotel alebo jednoducho Nekonečno izieb, končí. Hilbert ukázal, že všetky spočítateľné nekonečná sú rovnaké a akákoľvek manipulácia s nimi vždy ústi do nekonečna. David Hilbert zomrel v roku 1943 v Nemeckom Göttingene, no jeho dômyselnosť slúži dodnes každému z nás.
Prvé dve zákaznícke vlny elegantne vysvetlí aj toto video, po anglicky.





















































